Identifiant

ark:/13685/07096x01

Titre

Damiani Philosophi Heliodori Larissæi De Opticis Libri II : Nunc primum editi, et Animaduersionibus illustrati Ab Erasmio Bartholino Casp. Filio

Créateur

Héliodore de Larissa

Bartholin , Erasme

Rôle

Editeur

Date

1657

Éditeur

Parisiis : ex officina cramosiana

Siècle

XVIIe siècle

Format

Nombre de vues : 174

Notes

Suivi de remarques de l'éditeur.

Cote du document

7096x01

Licence

Licence Ouverte

Sur l'auteur

Bartholin, Erasme

Autre consultation

Consulter sur Internet Archive

Consulter en PDF

Identifiant SUDOC

Notice dans le Sudoc

Manifeste IIIF

https://numerabilis.u-pariscite.fr/iiif-presentation/3/item/214407/manifest

Table des matières

0001 - Page sans numérotation - [page de titre]

0003 - Page sans numérotation - [page de faux titre]

0005 - Page sans numérotation - Epistola

0014 - Page sans numérotation - Salve amice Lector

0022 - Page sans numérotation - Capita suppositionum opticarum

0023 - Page sans numérotation - Ta kephalaia tôn optikôn upotheseôn

0026 - Page sans numérotation - Summa Priuilegij Christianissimi Regis

0027 - Page 1 - [page de titre]

0028 - Page 2 - Damiani Philosophi Heliodori Larissaei De Opticis suppositionibus. Caput I / Caput II

0029 - Page 3 - Damianou Philosophou tou Eliodôrou lapissaiou, Peri optikôn ugotheseôn. Kaphalaion a / Kaphalaion b

0030 - Page 4 - Kephalaion g / Kephalaion d

0031 - Page 5 - Caput III / Caput IV

0034 - Page 8 - Kephalaion e

0035 - Page 9 - Caput V

0036 - Page 10 - Caput VI / Caput VII

0037 - Page 11 - Kephalaion z

0038 - Page 12 - Kephalaion è

0039 - Page 13 - Caput VIII

0040 - Page 14 - Caput IX / Caput X

0041 - Page 15 - Kephalaion th / Kephalaion i

0042 - Page 16 - Kephalaion ia

0043 - Page 17 - Caput XI

0044 - Page 18 - Caput XII

0045 - Page 19 - Kephalaion ib

0050 - Page 24 - Kephalaion ig

0051 - Page 25 - Caput XIII

0052 - Page 26 - Caput XIV

0053 - Page 27 - Kephalaion id

0062 - Page 36 - Tou autou, Peri optikôn biblion deuteron

0063 - Page 37 - Eiusdem De Opticis Liber secundus

0064 - Page 38 - Theorema I. Eorum quae cernuntur nihil simul totum videtur. Figura I

0065 - Page 39 - Theôrèma a. Oti ouden tôn orômènôn olon ama oratai

0066 - Page 40 - Theôrèma b. Tôn isôn megethôn en diasèmati keimenôn

0067 - Page 41 - Theorema II. Aequalium magnitudinum, & à se inuicem distantium, eae quae propiùs adiacent accuratius videntur. Figura II

0068 - Page 42 - Theorema III. Aequalium magnitudinum in eadem resta existentium eae quae ex maiori distantia videntur, maiores apparent

0069 - Page 43 - Theôrèma g. Ôse kai tôn isôn diasèmatôn

0070 - Page 44 - Theôrèma d. Ta parallèla tôn diasèmatôn ex aposèmatos orômèna

0071 - Page 45 - Theorema IV. Spatia parallela ex distantia aliqua visa inaequalis latitudinis apparent: & id spatium quod propius est semper apparet maius remotiori. Figura 4

0072 - Page 46 - Theorema V. Magnitudines rectangulae ex aliqua distantia visae, circumferentiae apparent. Figura 5

0073 - Page 47 - Theôrèma e. Ta orthogônia megethè ex aposèmatos orômèna pripherè phainetai

0074 - Page 48 - Theôrèma z. Kai tôn isôn megethôn, kai upô to auto omma keimenôn ta porrô meteôrotera phainontai

0075 - Page 49 - Theorema VI. Et aequalium magnitudinum quae sub oculo ponuntur, eae quae longius distant altiores apparent. Figura 6

0076 - Page 50 - Theorema VII. Si verò supra oculum constitutae fuerint magnitudines, eae quae longiùs distant, inferiores apparent. Figura 6

0077 - Page 51 - Theôrèma z. Ei de anôtron tou ommatos ta megethè keintai ta porrô mallon

0078 - Page 52 - Theôrèma è. Osa allèlôn iperekhei ipo to auto omma keimèna prosiontos

0079 - Page 53 - Theorema VIII. Magnitudinum quae sub eodem oculo positae sese inuicem superant; oculo appropinquante, maior magnitudino minorem excedere videtur maiore excessu, recedente verò videtur minore excessu superare. Figura 7

0080 - Page 54 - Theorema IX. Earum verò magnitudinum quae supra oculum constitutae sese inuicem superant, maior videtur minorem superare minori excessu ubi accesserit oculus, maiori verò ubi recesserit. Figura 8

0081 - Page 55 - Theôrèma th. Osa de allèlôn iperekhei epanô tou ommatos keimèna anisa megethè

0082 - Page 56 - Theôrèma i. Osa de allèlôn iperekhei ep' outheais elassoni megethei

0083 - Page 55 - Theôrèma th. Osa de allèlôn iperekhei epanô tou ommatos keimèna avisa megethè prosiontos

0084 - Page 56 - Theôrèma i. Osa de allèlôn iperekhei ep' outheias tô elassoni megethei

0085 - Page 57 - Theorema X. Si quaedam magnitudines sese superauerint, & accesserit oculus in eadem rectâ cum minori magnitudine, & recesserit; aequali portione semper apparebit maior minorem excedere. Figura 9

0086 - Page 58 - Theorema XI. Si oculorum distantia maior fuerit diametro sphaerae, ipsius sphaerae plus quàm dimidia pars videbitur: si verò distantia oculorum minor fuerit diametro sphaerae, minus apparebit dimidia eius parte: & si aequalis existerit diametro sphaerae, distantia oculorum, sphaerae pars dimidia in conspectum veniet. Figura 10

0087 - Page 59 - Theôrèma ia

0089 - Page 61 - Figura 11

0090 - Page 62 - Theorema XII. Si conus, cuius basis est circulus cui perpendicularis fuerit axis coni, ab uno oculo videatur, videbitur minus quàm dimidia coni pars. Figura 12

0091 - Page 63 - Theôrèma ib. Kôvou kuklov ekhontos tiô basin

0093 - Page 65 - Figura 13

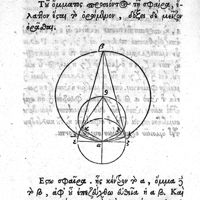0096 - Page 68 - Theôrèma ig. Tou ommatou prosiontos tè sphaira

0097 - Page 69 - Theorema XIII. Oculo accedente ad sphaeram, minor eius pars videbitur, et si maior appareat. Figura 14

0100 - Page 72 - Theôrèma id. Esi popos, ou tou ommatou methisamènou

0101 - Page 73 - Theorema XIV. Est locus aliquis ubi si transponatur oculus & maneat obiectum visibile, semper aequale apparebit. Figura 15

0102 - Page 74 - Theorema XV. Si magnitudino quaedam fuerit perpendicularis subiecto plano: constituto autem oculo in puncto aliquo plani, visibile transponatur in circuli circumferentia, cuius centrum est oculus; visibile semper aequale apparebit, obtinens parallelum situm ei quem initio habeat. Figura 16

0103 - Page 75 - Theôrèma ie

0104 - Page 76 - Theôrèma is

0105 - Page 77 - Theorema XVI. Si visibile non fuerit perpendiculare subiecto plano, atque existens aequale semidiametro circuli, transferatur secundum circuli circumferentiam; apparebit aliquando aequale, aliquando inaequale; semper obtinens situm parallelum ei quem ab initio habuit. Figura 17

0110 - Page 82 - Theorema XVII. Si obiectum visibile perpendiculare fuerit subiecto plano, & transferatur oculus in circumferenciâ circulu, cuius centrum est punctum in quo magnitudino insistit plano; visibile semper aeqale apparebit. Figura 18

0111 - Page 83 - Theôrèma iz

0112 - Page 84 - Theôrèma iè. Tôn isô takhei phenomènôn, ta porrô dokei braditeron phereatai

0113 - Page 85 - Theorema XVIII. Eorum quae aequali celeritate feruntur, ea quae longius absunt apparent tardius ferri. Figura 19

0114 - Page 86 - Figura 20

0116 - Page 88 - Theôrèma ith. Tod' ommatou mènontos, tôn de opseôn parapheromènôn

0117 - Page 89 - Theorema XIX. Oculo manente & circumlatis radiis, ea visibilia quae è longinquo sunt videntur relinqui. Figura 21

0118 - Page 90 - Theorema XX. Magnitudines quae augentur videntur ad oculum accedere. Figura 22

0119 - Page 91 - Theôrèma k. Ta auxanomèna tôn megethôn

0122 - Page 94 - Animadversiones in Libros opticorum Heliodori Larissaei

0162 - Page 136 - Ad Lib. II opticorum

0174 - Page 148 - Errores sic corrige